The Monty Hall Problem

The Monty Hall problem is a probability puzzle named after Monty Hall. He was the host of a US TV show called “Let’s Make a Deal”. On the face of it, this is an absurd paradox and many people simply refuse to believe the answer.

Introduction: The Monty Hall Problem

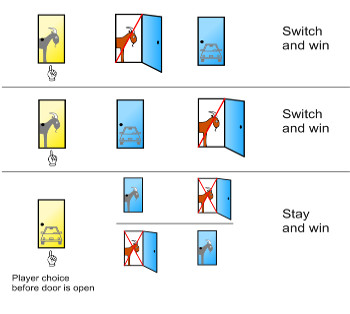
Now imagine that, like Alexander Drouz,  you’re on a TV game show. In front of you are three doors. You are told that behind one door is a car. Behind the other two are goats. You are asked to pick one door. Let’s say that you pick door number one. The host, who knows what’s behind each door, opens another door. Say number three. And there stands a goat. Monty Hall then says to you, “do you want to pick door number two?” The question is: should you stick with your original choice of number one or switch to number two?

Switch Please Monty

The answer to the Monty Hall problem is that you should switch. Why? Well if you stick with number one you’ll have a 1/3 chance of winning the car. If you switch to number two you’ll have better odds of 2/3. That doesn’t sound right! To you it appears that after one door is opened then there are two doors remaining to choose from. So both would have the same odds. But it’s just not true. This is the heart of the Monty Hall problem. After many plays it became obvious that those who switched won about 2/3 of the time and those who remained just 1/3 won. Online gambling news in the US says that even the famous Hungarian mathematician Paul Erdős was stumped, so don’t worry, you’re in good company.

Monty Hall Has Done The Hard Work

OK..now pay attention. The main point you must keep in mind is that Monty Hall curates the choices. He already knows where the car is. Look at it from another angle. Imagine you played the same game, but Monty Hall had no idea where the car was. Switching would make no difference and your odds would still be 50/50. The fact that he never chooses a door with the car is important. In a way he’s helping you, and raising the odds that switching is a good play. Try it with Free Spin Casino. Your odds will go up.

Let’s Go Large

Still not convinced. Let’s play a bigger game to see the Monty Hall problem more clearly. Imagine the same game but played with 100 doors. You pick a random door. Monty Hall then opens the other 98 doors. This leaves two doors, your random pick or the one left after Monty Hall eliminated all the others. Do you switch now? Of course you should. Your choice was just guess work giving you odds of 100/1. But now you have a filtered choice. Keep in mind that your original odds stay the same. But Monty has increased the odds by giving you the best door out of 98. And the “best” door is always going to give better odds than your “random” one. Easy. It’s not magic!

Monty Hall Says Back To School

Looking at the Monty Hall problem, it’s easy to see the common mistakes that novice gamblers make. Online gambling news in the US points out that these gamblers repeatedly treat non-random information as if it is random. They fail to understand whether they are in a strong or weak position from a statistical point of view. We can often see the gambler going against his own best interest from a basic lack of understanding of the statistical probability of an event. So before you gamble with real money, learn some simple math, in order to recognize the probability of an event repeating. Then hit Free Spin Casino. You’ll be happy you did.

Some History

Though we know this probability problem by the name of Monty Hall, the same experiment has been posed before. For example, in “Calcul des Probabilites”, a text written in 1889, Joseph Bertrand proposes his “Bertrand’s box paradox”. Here there are three boxes: a box with 2 x gold coins, a box with 2 x silver coins and finally, a box with one of each. A random box is chosen. One coin is withdrawn. It turns out to be a gold coin. So…what is the probability that the other coin is gold? Just as with the Monty Hall problem, everyone shouts 1/2 when the real probability is actually 2/3.

Monty Hall: Keeping it Real

One point of note is that Monty Hall did not necessarily follow the rules of his own game. Sometimes he didn’t allow the contestant the opportunity to switch. And sometimes he would open the losing door immediately. As he once said, “If the host is required to open a door all the time and offer you a switch, then you should take the switch. But if he has the choice whether to allow a switch or not, beware. Caveat emptor. It all depends on his mood.”